IEEE二进制浮点数算术标准（IEEE 754）

4381字约15分钟

2025-02-08

简介

IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。只有32位模式有强制要求，其他都是选择性的。大部分编程语言都有提供IEEE浮点数格式与算术，但有些将其列为非必需的。例如，IEEE 754问世之前就有的C语言，有包括IEEE算术，但不算作强制要求（C语言的float通常是指IEEE单精确度，而double是指双精确度）。该标准的全称为IEEE二进制浮点数算术标准（ANSI/IEEE Std 754-1985），又称IEC 60559:1989，微处理器系统的二进制浮点数算术（本来的编号是IEC 559:1989）。后来还有“与基数无关的浮点数”的“IEEE 854-1987标准”，有规定基数为2跟10的状况。最新标准是“ISO/IEC/IEEE FDIS 60559:2010”。

原码、反码、补码、移码

原码（Sign-Magnitude）

定义：原码是一种最简单的有符号数表示方法，最高位为符号位（0 表示正数，1 表示负数），其余位表示数值的绝对值。
计算方法：对于正数，原码就是其二进制表示；对于负数，符号位为 1，其余位为数值绝对值的二进制表示。
示例：假设使用 8 位二进制表示整数，+5 的原码是 00000101，-5 的原码是 10000101。
缺点：原码存在两个零（+0 和 -0），并且在进行加减法运算时需要额外处理符号位，增加了硬件设计的复杂度。

反码（One's Complement）

定义：反码是一种将负数表示为正数的方法，符号位不变，其余位取反。
计算方法：对于正数，反码就是其原码；对于负数，符号位为 1，其余位取反。
示例：假设使用 8 位二进制表示整数，+5 的反码是 00000101，-5 的反码是 11111010。
缺点：反码也存在两个零（+0 和 -0），并且在进行加减法运算时需要额外处理符号位。

补码（Two's Complement）

定义：补码是一种将负数表示为正数的方法，符号位不变，数值部分取反后加 1。
计算方法：对于正数，补码就是其原码；对于负数，符号位为 1，数值部分取反后加 1。
示例：假设使用 8 位二进制表示整数，+5 的补码是 00000101，-5 的补码是 11111011。
优点：补码解决了原码和反码存在的两个零问题，并且在进行加减法运算时不需要额外处理符号位。
缺点：补码的表示范围比原码和反码要小，因为补码的表示范围是原码和反码的一半。

移码（Excess-K）

定义：移码是在真值的基础上加上一个偏移量（通常为 $2^{n - 1}$ ，其中 $n$ 为编码的位数）得到的。移码的符号位与原码、反码、补码相反，即 0 表示负数，1 表示正数。
计算方法：将真值加上偏移量，然后转换为二进制表示。
示例：假设使用 8 位二进制表示整数，偏移量为 $2^{7} = 128$ 。+5 的移码是 10000101（ $5 + 128 = 133$ ，二进制为 10000101），-5 的移码是 01111011（ $-5 + 128 = 123$ ，二进制为 01111011）。
应用场景：移码常用于表示浮点数的阶码，因为移码可以方便地比较大小，使得浮点数的阶码可以像无符号数一样进行比较。

组成

在IEEE 754 格式浮点数由 3 个部分组成，分别是符号码，阶码，尾数码，对应部分所占位数如图 1-1 所示：

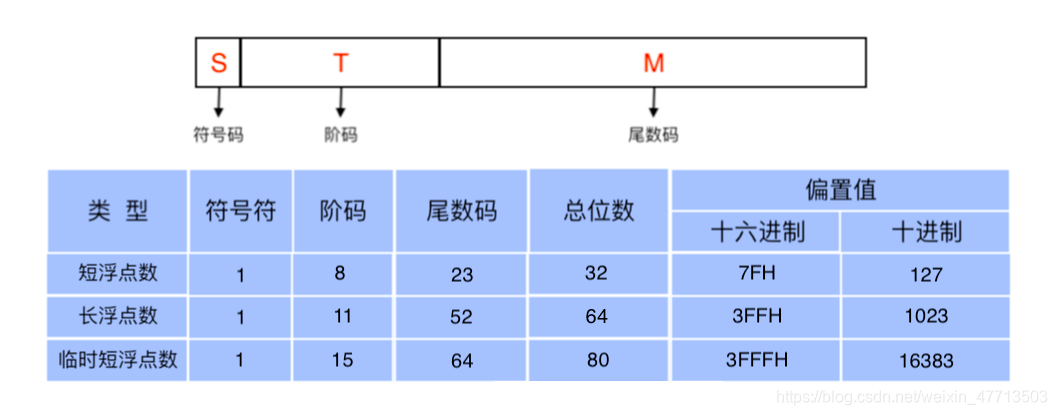
IEEE 754 标准分 3 个类型的浮点数：分别是短浮点数 float，长浮点数 double，临时短浮点数 long double，下面的讨论一律采用 float 类型进行。

1. 关于 IEEE 754 浮点数标准中的阶码

在 IEEE 754 浮点数标准中，阶码是用移码表示的，移码的定义：移码 = 真值 + 偏置值；

普通情况下，移码的偏置值为 $2^{n - 1}$ ， 8 位的移码的偏置值为 $2^{8-1}$ = 128D = 1000 0000B;

例如：-127D = -0111 1111B ，其移码为 -0111 1111 + 1000 0000 = 0000 0001；

在 IEEE 754 标准中，移码的偏置值是 $2^{n - 1} - 1$ ，8 位的移码的偏置值为 $2^{8-1} - 1$ = 127D = 0111 1111B;

例如：-126D = -0111 1110B ，其移码为 -0111 1110 + 0111 1111 = 0000 0001

提示

-127D 后面的字母 D 表示的是 Decimal（十进制），即表示 -127 是个十进制数，-127D 即为简写；

同样地，-0111 1110B 后面的字母 B 表示的是 Binary（二进制），即表示 -0111 1110 是个二进制数，-0111 1110B 即为简写；

注意

注意：8 位中，-127D 和 128D 这 2 个阶码有特殊用途，一般不在正常讨论范围（-126～127），他们的移码分别是：

-127D：-0111 1111 + 0111 1111 = 0000 0000；
128D：1000 0000 + 0111 1111 = 1111 1111；

2. 关于 IEEE 754 浮点数标准中的尾数

在 IEEE 754 浮点数标准中，尾数码部分采用原码表示，且尾数码隐含了最高位 1，在计算时我们需要加上最高位1，即 1.M，我们通过一个例子来表示：

例如：有一个浮点数，真值为 0.11B ，那么其简略版的 IEEE 754 标准表示为（忽略符号码和阶码）：

S(1) E(8) 100 0000 0000 0000 0000 0000

即当 0.11B 这个数在记录为 IEEE 754 标准浮点数时，会这样处理，令 0.11B = 1.1 * $2^{-1}$ B ，尾数码是 1.1000…，然后隐含最高位1，即 1 .1000…。

3.计算 IEEE 754 标准浮点数的真值

在上述内容的分析之后，再通过观察分析以下这个 IEEE 754 单精度浮点数格式表示的数，系统性了解如何计算出 IEEE 754 标准浮点数的真值：

上数分别对应图1-1的中 S（符号码，0 正，1 负），E (阶码) ，M (尾数数值)为：

确定符号位（S）：：1，

符号位位于最左边的第 1 位，这里符号位 (S = 1)，表示这个浮点数是负数。

确定阶码（E）：：100 0000 1

100 0000 1，阶码，其真值为：移码 - 偏置值 => 1000 0001 - 0111 1111 = 0000 0010 = 2D = 10B；

确定尾数（M）：M (黑色部分) ：010 0000 0000 0000 0000 0000

010 0000 0000 0000 0000 0000 表示这个浮点数的尾数部分，其真值为：被隐含的最高位1 + 0.尾数部分 => 1 + 0.01 = 1.01B = 1.25D;

通过对 S，E，M 的分析，我们可以计算出该浮点数的真值，即： $V = (-1)^S\times M\times2^E$

-1 * 1.25D * $2^{2}$ = -5.0D 或 -1 * 1.01B * $2^{2}$ = -101.0B = -5.0D

注意

为什么在计算二进制时，公式里 E 不用 10 要用 2?

在 IEEE 754 标准浮点数真值计算公式中，虽然 E 计算结果 0000 0010 对应的十进制是 (2D)，二进制是 (10B)，但不用 (10B) 而用 (2) 来计算，主要是因为指数运算的规则和计算机对数值的处理方式。

指数运算规则:

在数学里，指数运算 (a^b) 中的 (b) 代表指数，它是一个数值。在公式 $2^{E}$ 里，底数 (2) 是固定的，而 E 作为指数，需要是一个具体的数值。在进行指数运算时，我们习惯使用十进制数来表示指数，因为这样更符合我们日常的计算习惯。

例如， $2^{2D}$ 很容易理解为 $2\times2 = 4$ ，但如果写成 $2^{10B}$ ，就不符合常规的指数运算表达，而且容易引起混淆。实际上 $2^{10B}$ 这种写法是错误的，因为指数运算要求指数是一个数值，而不是二进制形式的表示。简单点说，就是 E 必须是十进制的数值。

5. 关于IEEE 754 标准浮点数的范围

最小绝对值

IEEE 754 单精度浮点型表示的的最小绝对值：尾数码全为 0 ，阶码真值为 -126D（对应的移码为 0000 0001B），此时整体的值为 1.0B * $2^{-126}$ D

最大绝对值

IEEE 754 单精度浮点型表示的的最大绝对值：尾数码全为 1 ，阶码真值为 127D（对应的移码为 1111 1110B），此时整体的值为 1.111…B * $2^{127}$ D

关于阶码真值为 -127 和 128

一般我们正常探讨的阶码区间是 -126D ～ 127D，而真值 -127D 的阶码为 0000 0000B，真值 128D 的阶码为 1111 1111B。

阶码真值为 -127

当阶码全为 0 ，尾数不全为 0，表示，用来表示比最小绝对值还要小的数，即

尾数码隐含的最高位不是 1，而是 0；
阶码真值固定为 -126，而非 -127；

非规格化小数

在 IEEE 754 浮点数标准中，非规格化小数（Denormalized numbers，也称为非正规数或次正规数）是一种特殊的浮点数表示形式，用于填补最小规格化数和零之间的数值间隙，从而提供更精细的数值表示。以下是关于非规格化小数的详细介绍：

1. 规格化数与非规格化数的背景

在 IEEE 754 标准里，浮点数由符号位（Sign）、指数位（Exponent）和尾数位（Mantissa）三部分组成。规格化数的尾数部分默认隐含一个前导 1，即形式为 $1.M$ ，其中 $M$ 是尾数位表示的小数部分。然而，这种表示方式无法表示非常接近零的数，为了填补这一数值间隙，引入了非规格化数。

2. 非规格化小数的表示规则

符号位（Sign）：与规格化数相同，0 表示正数，1 表示负数。
指数位（Exponent）：指数位全为 0。在单精度浮点数（32 位）中，偏移量为 127，此时指数的真值固定为 -126；在双精度浮点数（64 位）中，偏移量为 1023，指数真值固定为 -1022。
尾数位（Mantissa）：尾数部分不再隐含前导 1，而是以 $0.M$ 的形式表示，其中 $M$ 是尾数位表示的小数部分。

3. 非规格化小数的真值计算

非规格化小数的真值计算公式为：

$[V = (-1)^S \times 0.M \times 2^{-126} \text{（单精度）}]$
$[V = (-1)^S \times 0.M \times 2^{-1022} \text{（双精度）}]$ 其中， $S$ 是符号位， $M$ 是尾数位表示的小数部分。

当阶码全为 0 ，尾数全为 0，表示真值 +/- 0 ；

详情

在 IEEE 754 标准里，浮点数由符号位（S）、阶码（E）和尾数（M）三部分构成。“当阶码全为 0 ，尾数全为 0，表示真值 +/- 0” 这句话描述的是一种特殊情况，下面为你详细解释：

浮点数的一般表示

IEEE 754 标准下，浮点数的真值计算公式通常为 $V = (-1)^S\times(1 + M)\times2^{E - bias}$ ，这里的 $S$ 是符号位， $M$ 是尾数， $E$ 是阶码， $bias$ 是偏置值（单精度时 $bias = 127$ ，双精度时 $bias = 1023$ ）。

阶码全为 0 且尾数全为 0 的情况

当阶码（ $E$ ）全为 0 且尾数（ $M$ ）也全为 0 时，浮点数的表示就变得特殊了。此时，浮点数的真值取决于符号位（ $S$ ）：

符号位 $S = 0$ ：代表正零（+0）。
符号位 $S = 1$ ：代表负零（-0）。

为何会有正负零

在数学里，零是没有正负之分的。不过在计算机中，为了满足某些特定的计算需求，IEEE 754 标准引入了正负零的概念。正负零在数值上相等，但在某些运算中可能会产生不同的结果，例如在除法运算里， $1 / +0$ 会得到正无穷（ $+\infty$ ），而 $1 / -0$ 会得到负无穷（ $-\infty$ ）。

代码示例

// 正零的单精度 IEEE 754 二进制表示
const positive_zero_binary = '00000000000000000000000000000000';
// 将二进制字符串转换为 32 位无符号整数
const positive_zero_integer = parseInt(positive_zero_binary, 2);
// 创建一个 ArrayBuffer 用于存储 32 位数据
const positive_buffer = new ArrayBuffer(4);
// 创建一个 DataView 对象来操作 ArrayBuffer
const positive_dataView = new DataView(positive_buffer);
// 将 32 位无符号整数写入 DataView
positive_dataView.setUint32(0, positive_zero_integer, false);
// 从 DataView 中读取单精度浮点数
const positive_zero_float = positive_dataView.getFloat32(0, false);

// 输出：0
console.log(positive_zero_float); 
// 输出：+Infinity
console.log(1/positive_zero_float); 


// 负零的单精度 IEEE 754 二进制表示
const negative_zero_binary  = '10000000000000000000000000000000';
// 将二进制字符串转换为 32 位无符号整数
const negative_zero_integer = parseInt(negative_zero_binary , 2);
// 创建一个 ArrayBuffer 用于存储 32 位数据
const negative_buffer = new ArrayBuffer(4);
// 创建一个 DataView 对象来操作 ArrayBuffer
const negative_dataView = new DataView(negative_buffer);
// 将 32 位无符号整数写入 DataView
negative_dataView.setUint32(0, negative_zero_integer, false);
// 从 DataView 中读取单精度浮点数
const negative_zero_float = negative_dataView.getFloat32(0, false);

// 输出：0
console.log(negative_zero_float); 
// 输出：-Infinity
console.log(1/negative_zero_float);

注意：在 JavaScript 中，如果你直接使用 parseInt 函数将 10000000000000000000000000000000 转换为十进制，它会把这个字符串当作一个普通的二进制数进行转换，而不会考虑 IEEE 754 浮点数的规则。

const negative_zero_binary = '10000000000000000000000000000000';
const negative_zero_decimal = parseInt(negative_zero_binary, 2);
console.log(negative_zero_decimal); // 输出：-2147483648